Exactly-Once Delivery
Exactly-Once Delivery (EOD) is a very useful guarantee to have when designing a distributed system; being sure that no message is lost or delivered more than one time, despite all possible faults, makes the design of any distributed systems simpler. Intuitively, EOD is clear: we don’t want to lose or duplicate the data/operations. The exact definition, however, is not agreed upon in the community. As a result, there is a debate on whether EOD is possible or impossible to achieve. In this post, we focus on EOD, its possibility/impossibility, and what it really means in practice.
Outline
Fault-tolerance
We start this post by talking about fault-tolerance and how a practical fault-tolerant distributed system is supposed to behave in the presence of faults. Faults are the reality of distributed systems. Anything that can go wrong will
go wrong. Thus, when designing a distributed system, we must always consider
all possible faults and be prepared for them. However, if we consider all
sorts of faults and assume nothing is reliable how can we ever come up with a correct design?! For
example, if we assume that a channel is unreliable and theoretically can drop
all messages, how can we show the correctness of any system?
Safety and Liveness
The key to building practical distributed systems is the separation of safety
and liveness properties. Informally,
- A safety property requires that something bad must never happen.
- A liveness property requires that something good must eventually happen.
By this separation, we can design useful systems this way:
A practical distributed system must
- always guarantee safety even in presence of faults, and
- guarantee liveness when faults stop occurring for a long enough time after any arbitrary sequence of occurrences.
The first part is clear: we don't want the "something bad" defined by the
safety property to ever happen even in the presence of faults. The second
part, on the other hand, is a bit complicated. To prove that our design
satisfies our desired liveness property, we have to show that no matter what
sequence of faults occur in our system, if faults stop occurring for a long
enough time, the "something good" required by the liveness property will
eventually happen.
What is "long enough"?
That depends on the actual system. In practice, we can assume that faults
periodically become infrequent enough compared to time required for our
application to satisfy its liveness properties. When we want to prove the
correctness of a fault-tolerant design, we typically assume the faults
eventually stop occurring forever.
But doesn't assuming that fault will eventually stop occurring forever
makes the problem trivial?!
No. Although to prove the liveness we assume faults stop occurring, the
algorithm we design may never use that fact, as it does not know when faults
will stop occurring. A fault-tolerant protocol must guarantee that after any
arbitrary number of faults in any order it will eventually satisfy the
condition required by the liveness property. In other words,
We are allowed to assume that faults eventually stop, but we are not allowed to assume when that happens.
Why can't we use this assumption to prove the safety of a protocol? Why is it only useful for liveness?Safety properties can be violated in a finite execution. In other words, at some point in time, we can say "That's it, safety violated. That bad thing happened!". When we are reasoning about the safety of a system we cannot say "Don't worry, we assume faults stop before the bad thing happens". We cannot say that, because as we said above, we cannot make any assumption about when faults stop. That's why the assumption that faults eventually stop is not useful for safety properties.
If it is not clear to you at this time, I suggest you continue reading and come back to this section later.
Two Generals' Problem (TGP)
Before talking about message delivery guarantees, let's start with the classic
Two Generals' Problem (TGP) [1] that beautifully shows how the unreliable
nature of communication in distributed systems makes things challenging, even
things that initially might seem to be very simple.
Once upon a time, there were two generals who wanted to capture a city. They had camped outside the city, far from each other. They could capture the city, only if they both attacked at the same time, so they both had to be aware of the time of the attack decided by one of the generals. The only way of communication between them was through sending messengers. However, the messengers could be captured and killed! Thus, the generals couldn't be sure that their messages get delivered to the other side successfully.
|
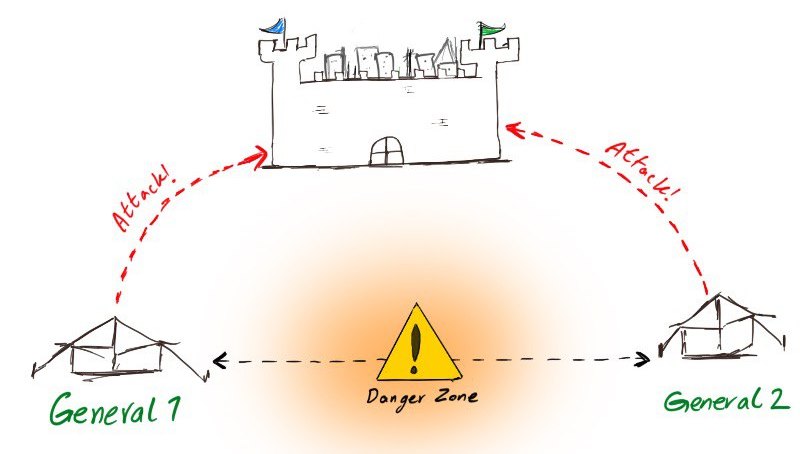
| Sketch 1. Two Generals' Problem (TGP). The generals must agree on the time to attack, but their only way of communication is through sending messengers who might be captured. |
The problem is to find a solution for these generals to attack together. Now,
let's see how we can view this problem as the problem of designing a
fault-tolerant distributed system. The capture of the messenger can be viewed as the
"fault" for the system. We divide the requirements of the problem as follows:
- Safety: No general must attack alone.
- Liveness: Generals must eventually attack.
Impossibility of TGP
If you try to solve this problem and carefully examine your initial
solutions, you will soon guess that this problem is probably unsolvable. The
impossibility of TGP is the result of the requirement of mutual guarantee
needed by the generals. The first general must make sure that the second
general is aware of the attack time, so it can go ahead and send a
messenger. However, due to the possibility of the messenger being captured,
the first general cannot be sure that the second general will receive the
message and attack. Thus, the second general must make sure that the first
general knows that the second general knows. The problem is not
solved even if we ask the second general to send an acknowledgement to the
first general, because the messenger carrying the acknowledgement also might
be captured. If the messenger makes it to the first general, now this is the
first general that needs to make sure that the second general
knows that the first general knows that the second general knows, and
it goes on and on! It is like that episode of Friends where Rachal and Phoebe find out
about Monica and Chandler secretly seeing each other, and both sides try to have a little fun using what the other side doesn't know.
Here, we prove that it is indeed impossible to solve TGP. Before proving the impossibility, we make the following observation:
Observation: Since the two generals have not agreed on the time to
attack, any solution to this problem MUST involve sending at least one
messenger between these two generals (i.e., you can't say I have a
solution that does not require sending any messenger!).
We first prove the impossibility of TGP with a fixed-length protocol, i.e., a protocol that ends
after sending a certain number of messages.
Proof (impossibility of TGP for fixed-sized protocols): Let's
assume there is a fixed-length solution S for this problem, i.e.,
solution S requires sending N messengers. Let's denote these
messengers with m1,m2,m3,...,mN. Now, suppose the sender of the last
messenger is general G2 and receiver is general G1. From the
perspective of G2, the protocol is done in its entirety, i.e., the
required N messages are sent. Thus, it goes ahead and decides to
attack. However, the last messenger might be captured. For solution S
to be correct, G1 must also decide to attack even though it didn't
receive message m(N-1). Thus, both G1 and G2 don't need message
m(N-1).
By repeating the argument above, we can conclude that the protocol
with zero number of messengers solves the problem which is
contradictory to the observation that generals must send at least one
messenger. ∎
The proof above shows that we cannot have a protocol that says "send these
N messages and you will be fine". But what about a protocol that its
length is not fixed. For example, consider the following protocol:
"G1 keeps sending messengers, until it receives an acknowledgement. G1 decides to attack when it receives the acknowledgement, and G2
decides to attack on the first messenger it receives from G1"
Based on the non-determinism of the faults, the above protocol may end after sending 2, 3, 4, or more messengers. Thus, before executing the protocol we cannot
specify an N as the number of messengers sent with this protocol. The
impossibility proof for this case is similar to fixed-size with a little
change.
Proof (impossibility of TGP for the general case):
Suppose there exists solution S that solves TGP. Based on the liveness
part of the requirement, we know for any execution E where faults stop
occurring, eventually both generals decide to attack. Slice the prefix P
of E where both generals have decided to attack. Now, consider execution
E' that has P' as prefix such that P' is identical to P except the last
messenger sent in P is captured in P'. After P', also all messengers
sent in E' are captured (see Figure 2).
|
|
Sketch 2. E and E' are indistinguishable from the
perspective of the sender of the last messenger which is G2
here. Thus, assuming that G2 decides to attack at point A, it
must also decide to attack at point B.
|
From the perspective of the sender of the last messenger sent in P (say
G2), P and P' are indistinguishable. Thus, it goes ahead and decides to
attack like in E. However, for the receiver of that messenger (G1), P
and P' are not the same. All future messengers will be captured in E'.
Thus, G1 cannot change its decision based on future messengers. For S to
be correct, G1 must also decide to attack even though it didn't receive
the last message sent in P. Thus, both G1 and G2 don't need that last
message.
By repeating the argument above, we can conclude that the protocol with
zero number of messengers solves the problem which is contradictory to
the observation that generals must send at least one messenger. ∎
You took prefix P form execution E where faults eventually stopped, and
used it to build E' where faults don't stop. Isn't it a problem? Shouldn't
P belong to an execution where faults stop?
Prefix P of an exaction where faults stop is indistinguishable from prefix
P' of an exaction where faults never stop, from the perspective of G2 as the
sender of the last messenger in prefix P. Whatever happened in E happens in
E' up to the point where G2 decides in E. Thus, assuming that G2 runs a
deterministic algorithm it must do the same thing in E'.
But why can't I assume faults stop and the second general will receive the time of the attack and will decide to attack at that time?As we said in the first section of this post, you can assume faults eventually stop, but you cannot assume when that happens. For example, the following algorithm does not satisfy the safety of TGP:
- The first general immediately decides to attack.
- the second general attack when it receives the order.
You cannot say "faults eventually stop and the second general will join the attack", because what if faults stop after the time of the attack? In that case the first general will attack alone which violates the safety of TGP. As we said in the first section, the assumption that faults eventually stop has no use for safety.
(Side Note: The Generals Paradox defined in [1] is different from TGP as we defined it here. Specifically, in [1], there is no time constraint for the generals to attack. Instead, the two generals only want to agree to attack or retreat. With that definition, [1] uses essentially the same proof as the one explained above to show the impossibility for the fixed-size case, but it argues we can have a variable-length (possibly infinitely long) solution for the problem. In other words, the problem is unsolvable only with a fixed-size algorithm. With the definition provided in [1], the problem does not have any safety requirements. In particular, instead of the safety requirement defined for TGP above, [1] only requires "When a general decides to attack, the other general will also eventually decide to attack" which is in fact, a liveness property. Here, on the other hand, we considered TGP with the time constraint, i.e., the attack will happen at a certain time by the decided generals. We showed above, in any case, variable or fixed, when generals are specifying a time to attack, TGP is impossible.)
At-Least-Once Delivery (AOD)
The processes in a distributed system typically talk to each other via
messages. Just as in TGP, in a distributed system, we can never be sure
that when we send a message, it will be delivered successfully. Suppose we
have a sender that wants to send a message to a receiver over an
unreliable channel. We want to make sure that receiver receives the
message despite the transient failures of the channel. It is OK if the
receiver receives the message more than one time, but at least one time it
must receive it successfully. That's why we call this problem
At-least-Once Delivery (AOD).
Initially, AOD might seem the same as TGP; the sender could be one of the
generals suggesting a time to attack that wants to make sure the other
general (i.e. the receiver) receives its message about its intention to
attack at a certain time. However, there is a big difference between AOD and
TGP. Unlike TGP, in AOD, the receiver does not need to make sure that the
sender is sure that the receiver has received the message. Thus, compared to
TGP, AOD is asymmetric, i.e., only one side needs assurance.
Unlike TGP, AOD is solvable. To prove that, it is enough to put a solution
on the table and prove that it is correct. Let's see what are safety and
liveness for AOD:
- Safety: Nothing
- Liveness: the message is eventually delivered to the receiver.
Solution for AOD: The sender keeps sending the message until it
receives an acknowledgement from the receiver.
|
|
Sketch 3. Providing AOD. Sender keeps sending the message
until it receives an acknowledgement from the receiver. |
Proof of correctness: We
don't need to show that the protocol satisfies any safety property.
For the liveness, we are allowed to assume that faults eventually stop
occurring. Since the sender only stops if the receiver has received
the message, assuming the faults will eventually stop, the receiver
will eventually receive the message. ∎
Exactly-Once Delivery (EOD)
With AOD, we might deliver the message to the receiver more than one time.
That might not be acceptable for some applications. For example, consider a
shopping website. The redelivery of a request from the client to the server
will cause a duplicate order which is not acceptable. For such an application
we need a delivery guarantee stricter than AOD.
We define the Exactly-Once Delivery (EOD) problem as follows: We have a sender
that wants to send a message to a receiver over an unreliable channel. We want
to make sure that receiver receives the message exactly one time despite the
failures of the channel.
Whit above definition, let's identify the safety and liveness of EOD:
- Safety: The message is not delivered more than one time to the receiver.
- Liveness: The message is eventually delivered to the receiver.
Note that the receiver may not "reject" a delivery. Any message that passes
through the network and is received by the receiver is considered delivered.
We want to make sure that the message is never delivered to the receiver
more than one time.
It is straightforward to see EOD is impossible if there is no way for the
sender to know the result of its previous attempts to deliver the
message.
Proof (impossibility of EOD if the sender may not know the result
of its previous attempts):
Suppose deterministic algorithm A satisfies EOD. Consider two
executions E and E'. In both executions, the sender sends the message. In
E, the message is delivered, but in E' message is lost. Based on the
assumption, there is no way for the sender to distinguish E from E'.
Since A is deterministic, the sender will make the same choice in both
E and E'. If the sender decides to retry, it causes duplicate delivery
to the receiver in E, thereby violating the safety. If the sender
decides to stop, it causes no delivery to the receiver in E', thereby
violating the liveness. Thus, any choice may either violate safety or
liveness for some possible execution which is a contradiction to
correctness of algorithm A. ∎
But what if there is a way for the sender to know the result of its previous
attempts. If the sender has such an ability, it is easy to see the following
solution satisfies both safety and liveness of EOD.
Solution for EOD: The sender uses its ability to determine the result
of its previous attempts. Once it makes sure that none of its previous
attempts has been delivered or will be delivered, it resends the message and
repeats this process until it makes sure the message is delivered.
OK, EOD is possible if the sender can know the result of its previous
attempts, but how can it know that?
Asking the Receiver
One way to know the result of the previous attempts is by asking the
receiver. But this approach has two requirements:
- The receiver must know the answer. Thus, the receiver may never forget that a message is delivered once it is delivered.
- The channel between sender and receiver may never deliver messages out of the order. We refer to this as FIFO here, but note that the channel is still allowed to drop some messages. The requirement is that it can never deliver message M2 before M1, if M1 is sent before M2.
With these assumptions, we can solve EOD as follows.
Solution for EOD: The sender sends the message for the first
time and the proceeds as follows:
- The sender keeps asking the receiver "Have you received the message?", until it receives a response from the receiver.
- The sender resends the message and goes to step 1, when it receives a "No" to the last "Have you received the message?" question that it sends to the receiver.
- The sender stops, when it receives a "Yes".
|
| Sketch 4. Providing EOD by asking the receiver. The sender waits to receive a "No" to its last "Received?" question before resending the message. |
Proof of correctness: The sender keeps resending the message until the message is delivered to the receiver. Thus,
the liveness of EOD is satisfied. The sender never resends the message, unless it receives a “No” to its last question. Since the channel is FIFO, and the question is sent after sending the previous messages, when the receiver receives the question, the previous messages must have been either permanently lost or delivered to the receiver. If the message has been delivered, the receiver would remember it and would answer “Yes”. Thus, when the receiver responds “No” to the last question, we know that all previous attempts to deliver the message have failed. Thus, the sender resends the message, only if none of previously sent messages is or will be delivered to the receiver, so the message is never delivered to the receiver more than one time that guarantees the safety of EOD. ∎
To make sure that a "No" is an answer to the last question sent by the
sender, the sender can attach an identifier to its question, and the
receiver attaches the same identifier to its response. The sender, then,
ignores any "No" that has an identifier different from the identifier of the
last question it sent.
Using an Intermediary
Sometimes we don't like the sender to be involved in the complications of FIFO communication and EOD protocol. Instead, we like to let the sender simply keep repeating until it receives the acknowledgment. In this case, we can use an intermediary between
the sender and receiver and provide EOD as
follows.
Solution for EOD with intermediary: Between sender and receiver
we have an intermediary. The channel between the sender and intermediary
is not required to be FIFO. But the channel between the intermediary and the receiver
is FIFO. The three parties proceeds as follows:
- The sender runs the AOD protocol.
- The receiver runs the EOD protocol.
- The intermediary runs a mixture of AOD and EOD as follows:
- It sends the question "Have you received the message?" to the receiver every time it receives the message from the sender.
- When it receives "No" to its last question, it sends the message to the receiver.
- It sends the acknowledgement of AOD protocol to the sender once it receives the "Yes" of the EOD protocol from the receiver.
|
| Sketch 5. Providing EOD using an intermediary. The intermediary runs AOD with the sender, and EOD with the receiver. We will have EOD from sender to receiver. |
I leave the proof to you. It must be easy to show the solution above satisfies both safety and liveness of EOD. The process done by the intermediary shown
in Sketch 5 is commonly referred to as deduplication.
EOD and TGP
If you search the web for EOD, you might encounter claims that EOD is the same
or as hard as TGP, so it is impossible. However, these claims are not
accompanied with formal definitions of these problems and the exact reduction supporting them.
As we showed above EOD, as we defined here, is possible while TGP is
impossible. Thus, the claim that EOD is as hard as TGP is not
correct.
But what about the following reduction?
Assuming we have EOD, we can solve TGP as follows:
- One general runs the sender side of EOD and the other general runs the receiver side of EOD.
- One general decides to attack when the sender decides to stop sending messages.
- The other general decides to attack when the message is delivered to the receiver.
Now:
- From the liveness of EOD, we know the message will be delivered.
- From the safety of EOD we know the sender must stop when the message is delivered to the receiver. Otherwise, the message will be delivered more than one time and safety of EOD is violated.
Thus, generals will eventually attack and no general attack
alone.
There is a flaw in this reduction. That is correct that when faults stop, the sender must stop at some point. Otherwise we will have duplicate delivery to the receiver. However, there is no guarantee that it happens before the time of the attack. The message might be delivered to the
receiver and the sender may never stop even after the attack is started by the receiver general. Thus, with the above reduction, the receiver general may attack alone that violates safety of TGP. In fact, we
used this scenario to prove the impossibility of TGP for the variable length
algorithm above.
Another way of looking at the difference between these two is this: we have a deadline in TGP, but we don't have any deadline in EOD. In TGP, when a general decides to attack, we have a limited amount of time for the second general to decide before the time of attack arrives. If due to communication failure, the second general does not decide by the time of the attack, the safety is violated. On the other hand, we don't have any deadline in EOD. Thus, when the message is received by the receiver, there is no deadline for the sender to find it out and stop.
EOD in Practice
We defined EOD and provided some solutions for it above. However, we left the
notions of "sender" and "receiver" abstract above. What are the sender and
receiver in practice ? Let's start over and review why someone might need EOD?
We typically need the delivery guarantees in the context of a client-server
application. In this setting, the server has a state. The client can
change the state of the server by sending requests to it. For example, in the
shopping website application that we talked about before, the server is the
website that maintains the set of orders as its state. When the client sends
its order to the server, we want to make sure we add exactly one order to the
state; we don't want to lose it or create duplicate orders.
As the example above shows, in a client-server communication, the real
receiver that we are interested to provide EOD for is
the state of the server. Otherwise, we don't want EOD! To realize why, suppose we consider the
server itself (not its state) as the receiver. Suppose we provide EOD for this
receiver. Now, suppose the server receives a request from the client, but then
it crashes before adding the order to its state. In this situation, since we
are providing EOD for the server, we are guaranteed that we never deliver the
order to the server again, so we will lose the order which is
unacceptable.
EOD with the state as the receiver is the only useful EOD. Otherwise, you
probably don't want EOD.
Instead of being the receiver, the server is the best candidate to play the
role of the intermediary, as we can have a FIFO channel between the server and its
state (see Sketch 6). Note that, here, we limit our discussion to having a single intermediary. A server with multiple writer threads is basically a design with multiple intermediaries. Additional care must be taken when we have multiple intermediaries.
The scheme shown in Sketch 6 is sometimes referred to
as Exactly-Once Processing (EOP), as the server is
guaranteed to process and apply the effect of each message to the state
exactly one time. Some people differentiate between EOP and EOD. However, EOP
can be considered as a special case of EOD with the state as the receiver. As
explained above, in practice, EOP is the guarantee that we really look for
when we want EOD.
|
|
|
Now, let's see what is the "Have you received the message?" question in
practice, having the server as intermediary and its state as the receiver. In
this setting, that question translates to the ability of the server to look at the state and figure our if a certain
message is delivered or not. The server can do it implicitly or explicitly.
Implicit delivery checking: In this approach, the server looks for the
effect of a given message on the state and figures out if it is
delivered or not. Suppose the message is a write operation to a database. The
server can make a query to the database and see if the effect of the write is
already applied to the database or not.
Explicit delivery checking: In this approach, the delivery of a message
is explicitly recorded on the state as a separate fact. In practice, we
want to transfer a series of messages instead of only one message. Thus, this
approach requires some way to identify messages. The following are some of the
common ways.
- If the messages are naturally ordered we can use the index of each message in the order as its ID. For example, when we are ingesting data from a Raft log or Kafka [2].
- We can use the hash of the message content [3].
- We can also simply add random GUIDs to messages on the client side. Just long enough random GUIDs are shown to work very well in practice.
The important thing to note with this approach is that delivering the
message to the state and recording the delivery must be done atomically and
instantaneously, i.e., there may not be a situation where the message is
delivered, but if you read the state you don't find its delivery being
recorded.
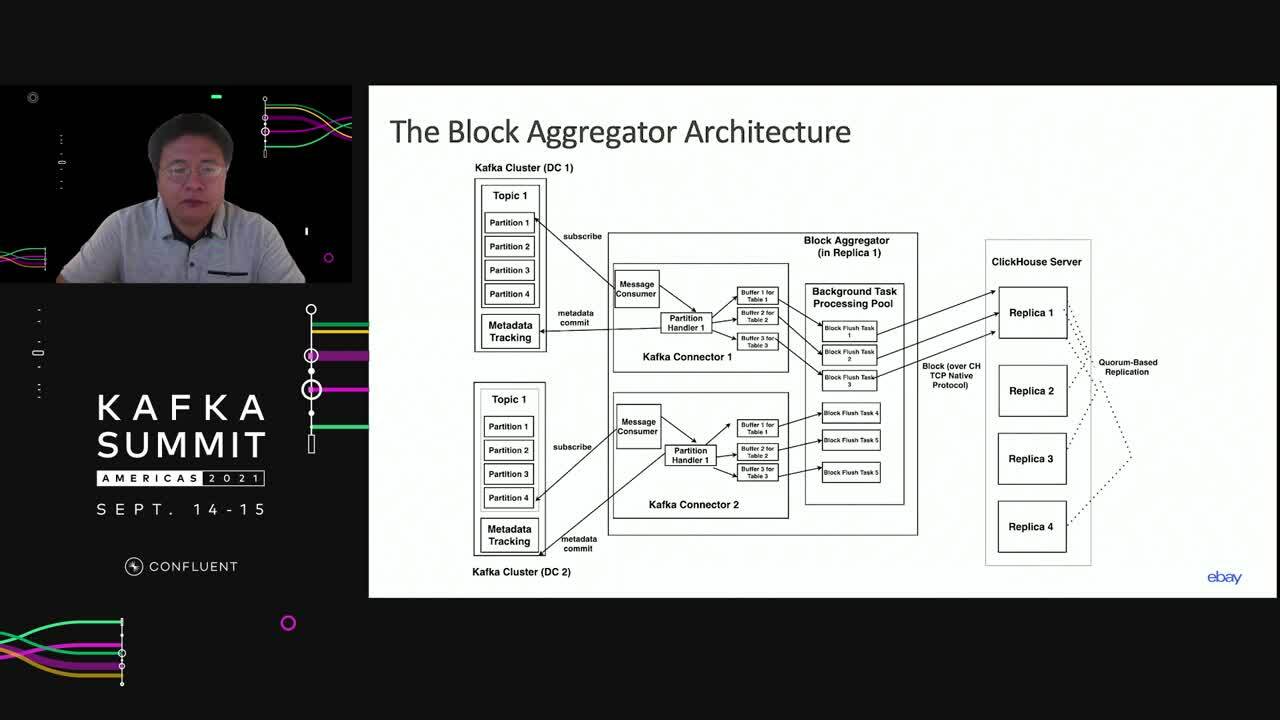
Example: Data Ingestion From Kafka to ClickHouse
In this section, as an example for the use of EOD in practice, we briefly
review the data ingestion from Kafka to ClickHouse using Block Aggregator
[4]. ClickHouse is a columnar store optimized for analytics. Since a columnar
store stores data column-by-column instead of row-by-row, it is critical to
load data in large blocks. Otherwise, the write throughput will be very bad,
because for a single row, a columnar store must store data in multiple
different locations, one per column. ClickHouse provides deduplication for
blocks of data using the explicit approach explained above. It uses the hash
of the content of each block to identify it. It guarantees that the visibility
of a block and recording its hash on Zookeeper is done atomically. Thus, by
checking the hash of the block on Zookeeper, it can determine whether a block
is delivered or not.
|
| Sketch 7. Deduplication by ClickHouse |
Sketch 7 is an implementation of EOP design shown in Sketch 6. To consume from Kafka, however, we need an additional component to form the blocks. The job of the Aggregator is to consume data from Kafka, accumulate Kafka
messages to form large blocks, and send them to the ClickHouse. Thus, the Aggregator plays the role of client in Sketch 6. As we said above, the client runs AOD, so it might need to resend the message when it times out while waiting for acknowledgement. To enjoy the deduplication provided by the ClickHouse, the
Aggregator must make sure to recreate identical blocks when it
wants to resend the data to the ClickHouse. Aggregator does that by storing metadata about how it
forms blocks, back to Kafka. This way, upon failure and recovery it can
deterministically replay what it did before and recreate identical
blocks.
|
|
Sketch 8.
Ingesting from Kafka to ClickHouse |
If you are interested to learn more can you refer to [4] or watch this talk.
Idempotence
As we said above, in practice, the purpose of EOD is to make sure each
request is applied to the state of the server exactly one time. It is
important, because we don't want to lose a request or apply its effect
more than one time. But what if delivering a request more than one time
does not change anything? For example, suppose our request is to set the
value of a key to a certain value. Delivering this request more than one
time does not make any difference compared with delivering it exactly
once. i.e., the requested operation is idempotent. When we have
idempotency, EOD is not practically needed. Thus, we don't need to
identify messages and determine whether we have delivered them or not.
Instead, we can use at-least-one delivery and it will be indistinguishable
from EOD.
It is common in the community to refer to what we did in Sketch 6 as "making
operations idempotent". Specifically, the message that we send to the
server can be considered idempotent as sending a message more than one time
does not take any additional effect. That is fine. However, it might be more
useful to reserve the term "idempotent" for operations that are naturally
idempotent. For example, there is an inherent difference between a SET
operation and an INSERT. The SET operation is naturally idempotent. We don't
need to be careful to avoid duplications. But INSERT operation needs
special treatment to look idempotent. We refer to that special
treatment as EOD.
Summary
In this post, we looked into the problem of message delivery in a
distributed system over an unreliable network. We focused on EOD and saw how
it is related to classic TGP. Unlike TGP, EOD is possible. Despite
similarity between TGP and EOD, these two problems differ in the symmetry
between two sides of the communication. Specifically, TGP requires mutual
assurance which is impossible to achieve assuming the omission of the
channel. On the other hand, in EOD, the message can be delivered without the
other side being aware of it and can remain in that state forever without
violating safety or liveness of EOD. We saw how EOD can be achieved in
practice, and saw when we want EOD, we really want it having the final
application state as the receiver. Otherwise, EOD will result in losing
client requests and is not desirable.
References
[1] James N. Gray, "Notes on database operating systems." In Operating
Systems, pp. 393-481. Springer, Berlin, Heidelberg, 1978.
[2] Mohammad Roohitavaf, Kun Ren, Gene Zhang, and Sami Ben-Romdhane.
"LogPlayer: Fault-tolerant Exactly-once Delivery using gRPC Asynchronous
Streaming." arXiv preprint arXiv:1911.11286 (2019).
[3] ClickHouse block de-duplication,
https://clickhouse.tech/docs/en/engines/table-engines/mergetree-family/replication/
[4] Mohammad Roohitavaf and Jun Li, Block Aggregator: Real-time Data
Ingestion from Kafka to ClickHouse with Deterministic Retries.
Comments
Post a Comment