Availability Modeling

Availability is one of the most important aspects of every service. The failure of a critical service can result in the unavailability of the final application for end-users, thus promptly impacting the company's revenue. That is why businesses usually care about availability more than other aspects of a service such as consistency, and in the trade-off between these two, under the CAP theorem, they usually favor availability. Being of utmost importance, it is critical for distributed systems and site reliability engineers to understand how their design or operational decisions affect availability of their service.

The typical approach to study availability is to have a mathematical model of availability. Using this model, for example, we can estimate the required number of replicas for our database to make sure we provide a certain level of availability. Although service providers usually do not invest in rigorous models for their services, some form of a model (at least a sketch of it in developers' minds) always exists in any reasonable team. Usually, service providers, especially those that provide services to internal customers (i.e., other teams inside a company) with less strict SLAs, have a back-of-the-envelope calculation of availability of their service and by over-provisioning resources, they make sure they hit the required level of availability. The amount of over-provisioning at big tech companies is usually a lot, scarifying hardware efficiency for higher availability.

I believe, however, having more rigor in modeling availability helps teams make better design decisions and increase their hardware efficiency. That is more critical for companies with smaller profit margins and especially for the cloud providers, as slightly higher efficiency (while keeping the promised SLA) may translate to significant savings for them.

In this post, I share some thoughts on availability and try to provide a practical definition for availability. We will also see how we can model and estimate availability for a service with the given definition.

Defining Availability

If you look at typical SLAs, even among services provided by the same company (e.g., SLAs for AWS services), you will see they vary significantly in how they define availability. If you are working on a team that provides a service, I suggest you go ahead and ask engineers in your team about availability of your service. There is a good chance that you will find out they are not on the same page on what availability means for your service either.

To understand challenges in defining availability, let's jump right in and try to calculate availability for the simple service shown in Sketch 1. In this system, we have a set of stateless app servers that receive a load balanced traffic. To process a request, an app server accesses one of the database replicas. Suppose, replicas are identical and we can read and write on any of them.

Sketch 1. A simple service. To process a request, an app server accesses one of the available database replicas.

Intuitively, it should be easy to define availability; we say our system is available, whenever it is able to successfully process requests. To successfully process a request, we need at least one app server and one database replica. So, how about modeling availability in terms of availability of its app servers and database replicas as follows?

Psuccessful_request = (1 - (1 - Aapp)5) (1 - (1 - Adatabase)3)             (1)

Let's break that down:

• Aapp and Adatabase are the probabilities of an app server and a database replica to be healthy. Suppose we know these two based on historical observations.
• (1 - Aapp) and (1 - Adatabase) are probabilities of of an app server and a database replica to be down.
• The probability of all 5 servers to be down, assuming their failures are independent, is (1 - Aapp)5.
• Thus, the probability of having at least one healthy app server is (1 - (1 - Aapp)5).
• Similarly, the probability of having at least one healthy database is  (1 - (1 - Adatabase)3). 
• The probability of service to be available is the probability of having at least one healthy app server and one healthy database replica at the same time, so we multiply these probabilities, i.e., (1 - (1 - Aapp)5) (1 - (1 - Adatabase)3) to calculate Psuccessful_request.

Psuccessful_request is the probability of having at least one app server and one database replica available. In that situation, if you send a single request, when there is no other request, your request is expected to be processed successfully. However, considering the service to be available with that definition completely ignores the capacity of our service. To understand why capacity is important, suppose the capacity of a database replica in Sketch 1 is 6 kqps, i.e., this single replica can handle 6000 requests per second. Extra requests will be rejected (i.e., they will receive a 503 error). Suppose one app server and one database replica are available. If we define availability as above, our system is considered to be available in this situation. Now, suppose the traffic to the system is 7 kqps. Since the database replica can handle only 6000 queries, 1000 requests are being rejected every second, i.e., the system is unavailable for 1000 requests per second while we are considering our services as "available"!

But isn't capacity a separate issue? The system is available, but it cannot handle that capacity. Aren't these two, two different aspects?

What matters is in the contract between you and your customer, and how we define availability must be based on that. If you told your customer we will handle 7 kqps, but due to a failure, you are handling only 6 kqps, you are being unavailable for 1 kqps. It does not matter how your system looks like while you are rejecting 1000 requests per second. All that matters is that from the perspective of the client you are being unavailable for that many requests per second.

As you can see, defining the system as available if it can handle a single request in vacuum is very misleading and has no practical value. Now, the question is, "Then, how should we define availability? When can we say our service is available and when it is not?"

Practical Definition of Availability

I believe, instead of categorizing the service as either available or unavailable at any given moment, it is better to define availability in terms of the fraction of successful requests to all request for any given period of time. A successful request is a request for which our service does not return a server error indicating an issue with your service. Thus, we define availability as follows.

A = Nsuccessful_requests / Nall_requests

We can use the equation above to define availability for any time interval that we want. In that case, for the number of successful requests and all requests, we only consider requests sent in that time interval. An example of a service with this definition of availability is Amazon DynamoDB. It defines availability for 5-min intervals as follows.

Definition of availability for Amazon DynamoDB:

• "Availability" is calculated for each 5-minute interval as the percentage of Requests processed by DynamoDB that do not fail with Errors. If you did not make any Requests in a given 5-minute interval, that interval is assumed to be 100% available.
• An "Error" is any Request that returns a 500 or 503 error code, as described in DynamoDB Common Errors on the AWS Site.

So in the above equation, DynamoDB considers requests sent in each 5-min interval, and calculates availability of that interval as the fraction of successful requests to all requests. It then computes the average of these 5-min availabilities as the "Monthly Uptime percentage". The SLA guarantees 5 9s monthly uptime and they refund the customer when the monthly uptime percentage fall bellow 5 9s.

There is a subtle yet important point about Nall_requests: Usually, we have a contract with customers on how many requests they can send to our service. When calculating availability, we have to exclude those requests that are exceeding the agreed upon request rate. Thus, instead of Nall_requests we use Nconsidered = min(Npromised, Nall_requests) to calculate availability, where Npromised is the number of requests we promised to be able to process for that time interval. By taking minimum, we are considering requests to the system up to the maximum number of requests we promised to be able to handle.

A = Nsuccessful_requests / Nconsidered                (2)

Modeling Availability

Violating SLA is not good for server providers. A good provider at least refunds customers which cost money (e.g., Amazon DynamoDB refunds the customers via service credit when the uptime falls below promised 5 9s (see the table in this page)). A provider that does not address SLA violation simply damages its reputation as a reliable service provider which results in higher cost in the long run. In any case, service providers need to make sure they don't violate their SLAs. Thus, it is critical for them to have an insight on how their design decisions and resource allocation affect availability of their service. In this section, we want to see how we can model and estimate availability.

Let Npossible_requests be the number of requests that our service can successfully handle in the time period for which we are calculating availability. So, Nsuccessful_requests equals min(Npossible_requests, Nconsidered), because we cannot handle more than Npossible_requests. Let's use this value in equation 2.

A = Nsuccessful_requests / Nconsidered

A = min(Npossible_requests, Nconsidered)  / Nconsidered

A = min(Npossible_requests/Nconsidered, Nconsidered/Nconsidered)

A = min(Npossible_requests/Nconsidered, 1)

Assume the capacity of our system is fixed during time t, i.e., our system is able to process C queries per second during time t. In that case, we can process a total number of C.t requests during time t. Similarly, suppose number of requests sent per second during time t is fixed. Let W denote this fixed rate. Thus, our service receives W.t requests during time t. Let Wpromised be our agreed-upon request rate with the customer. Thus, the rate that we consider is min(W, Wpromised), so we consider the incoming rate up to the maximum rate we promised to handle.

A = min(Npossible_requests/Nconsidered, 1)

A = min(C.t/min(W, Wpromised).t, 1)

Let's drop t:

A = min(C/min(W, Wpromised), 1)                (3) [fixed capacity and workload]

Ok, so given the capacity of our service and the current workload, we have a formula to calculate the availability. In practice, however, both capacity and workload can change; capacity may change due to failures or maintenance operations (e.g., we may lose a replica), and workload may change by clients' behavior. To deal with variable capacity and workload, let's estimate availability using expected value as a function of workload as follows.

A(w) = E[min(C/min(w, Wpromised), 1)]

A(w) = Σipi.min(ci/min(w, Wpromised), 1)                    (4)

Let's break down equation 4:

• First of all, note that we are estimating availability as a function of the workload. Thus, in practice, we use this definition this way: "If we operate at x queries per seconds, then the expected value of our availability is y". Thus, a service may provide 5 9s of availability if it operates at A queries per second, and only provides 4 9s if it operates at B queries per seconds. (If that sounds odd to you, go back and read the previous section to see how do we define availability)
• Our service can be in different states based on what components are failed and what components are healthy. For example, we have a state without no failure, a state with one database replica failure, a state with two database replica failures, etc. pi is the probability of being in state i.
• ci is the capacity of our system in state i. For example, let state 1 be the state where we don't have any failure in the system. Then, c1 is the capacity of our system in that state.
• To calculate the expected value of availability, we multiply availability in each state by the probability of that state and add all results for all states together.

If we want, we can get rid of workload (w), we can consider availability when the customer is utilizing its maximum agreed upon limit (i.e., w = Wpromised). 

A = Σipi.min(ci/Wpromised, 1)            (5)

Examples

Let's see some examples to see how to use equation 4

Single Server

Let's start with a very simple service with only one server. Suppose Mean-Time-To-Failure (MTTF) of this server is 15 days, i.e., we anticipate that this server goes down twice a month. Suppose Mean-Time-To-Recover (MTTR) of it is 30 min, i.e., once failed, it takes 30 minutes to recover. We can estimate MTTF and MTTR based on historical data of our server. Suppose the capacity of our server is 6 kqps.

Our system can be in two states. We calculate the probability and capacity of each state. 

1. The server is up: 
• Probability of this state is pup = MTTF / (MTTR + MTTF) = 15×24×60/(15×24×60 + 30) = 0.99
• Capacity of this state is cup = 6 kqps
2. The server is down: 
• The probability of this state is pdown = 1 - pup
• Capacity of this state is cdown = 0

Now, let's apply equation 4:

A(w) = Σipi.min(ci/min(w, Wpromised), 1) 

A(w) =  pu.min(cup/min(w, Wpromised), 1) + pdown.min(cdown/min(w, Wpromised), 1)

A(w) = MTTF / (MTTR + MTTF).min(cup/w, 1) + 0

A(w) = 0.99Min(6/min(w, Wpromised), 1)

Let's see what the calculated availability function implies for some scenarios:

• Suppose we have promised 6 kqps for our service. In that case, disregarding the workload, we provide 2 9s of availability. For example, if the customer is using 6.1 kqps, we still provide 2 9s of availability, as we are not responsible for the extra 0.1 kqps, and it is excluded in the way we calculate availability.
• Suppose we have promised 6.1 kqps. In that case, if the customer is using less than 6 kqp, we still provide 2 9s of availability.
• Suppose we have promised 6.1 kqps, and the customer is utilizing the promised 6.1 kqps. In that situation, our availability drops to one 9 (0.99*6/6.1 ~ 0.9)

Two Servers

Now, suppose we have two servers with the same MTTF and MTTR, and calculate availability. In this case, we may have zero, one, or two server failures. We calculate the probability and capacity in each state.

1. No server is down:
• Probability: pno_down = pup.pup = p2up
• Capacity: cno_down = 2cup = 1.2 kqps
2. One server is down:
• Probability: pone_down = pup.(1 - pup) + (1 - pup).pup = 2(pup - p2up)
• Capacity: cone_down = cup
3. Two servers are down:
• Probability: ptwo_down= (1 - pup)2
• Capacity: ctwo_down = 0

Let's apply equation 4:

A(w) = Σipi.min(ci./min(w, Wpromised), 1)

A(w) = pno_down.min(cno_down/min(w, Wpromised), 1) + pone_down.min(cone_down/min(w, Wpromised), 1) + 0

A(w) = p2up.min(2cup/min(w, Wpromised), 1) + 2(pup - p2up).min(cup/min(w, Wpromised), 1)

A(w) = 0.98.min(1.2/min(w, Wpromised), 1) + 0.0198.min(6/min(w, Wpromised), 1)

With this additional server, if we still promise just 6 kqps for our service, we provide 3 9s of availability, i.e., one 9 more than what we can provide with just a single server. The additional availability is not guaranteed if we increase our promised capacity.

Modeling Complicated Services

In practice, the architecture of a service is more complicated and involved than the examples discussed above. Figuring out the state space and calculating probability and capacity for each state could be difficult for some systems. In this section, I talk about two solutions for dealing with those cases.

Petri Nets and Markov Models

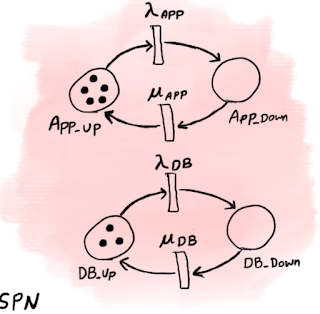
Petri nets are an interesting way to graphically model distributed systems. To model performance/availability measures, we need extensions of Petri nets such as Stochastic Petri Nets (SPNs) or Stochastic Activity Networks (SANs). These stochastic models are mapped directly to Markov processes. Explaining Petri nets and Markov processes is out of scope of this post, and I may write about them in future posts, but just to give a sense of how modeling with Petri nets looks like, Sketch 2 shows the SPN model and part of the corresponding Markov chain of the system shown in Sketch 1.

Sketch 2. The SPN model and part of the Markov chain of the system shown in Sketch 1. Note that not all states and transitions of the Markov chain are shown.

In the SPN model, places App_Up and DB_Up keep track of healthy app servers and database replicas, respectively. Each token in App_Up (or DB_Up) represents one healthy app server (or database replica). Similarly, App_Down and DB_Down keep track of failed app servers and database replicas. Initially, we have 5 healthy app servers and 3 healthy replica servers. The app server fails with rate λApp and recover with rate μApp. Database replica fails with rate λDB, and recover with rate μDB. Each possible position of tokens is called a marking. For example, in the initial marking, we have 5 tokens in App_Up and 3 tokens in DB_Up. Another marking is when we have one failed app server, so we have 4 tokens in App_Up, one in App_Down, and 3 in DB_Up. We can assign a reward for each marking. In our case, we compute the capacity C in each marking, we set the reward to min(C/min(w, Wpromised), 1) (equation 3), as we like to compute the expected value of this variable for the given workload w.

In the corresponding Markov chain, each state corresponds to a marking of the SPN model. For example state {App=5, DB=3} corresponds to the initial state of the SPN model. Based on rates of the SPN model, the system transitions in the corresponding Markov chain from the state representing the initial marking to a state representing the new marking after transition of the SPN model.

Once you have the model, you can use a tool to solve the model and compute the expected value of the reward based on transient or steady-state (long term) probabilities. These tools use different techniques to solve the model and calculate the measures that you are interested in. Two of my favorite tools that I have used in the past are Möbius and Oris.

I have found Petri nets very powerful and useful for modeling distributed systems. However, one issue with modeling with Petri nets (and all state-based solutions) is state space explosion which mean the number of states to consider quickly grows such that solving the model is not tractable anymore. Specifically, when we have N components each of which can be either healthy or failed, we have 2^N states in total (i.e., the state space grows exponentially). Another issue engineers' unfamiliarity with these formalisms. Thus, you may have a hard time communicating them with the rest of the team, or expecting other engineers to use or maintain them. In those cases, maybe simulation is a better option.

Monte Carlo Simulation

The idea of Monte Carlo simulation is to randomly sample the system and draw some numerical results about the metrics we are interested in. With a large number of samples, we can estimate the metrics with good confidence. The following is a sketch of Monte Carlo simulation to calculate availability.

repeat M times {

• Using a random number and the availability distribution of each of the N components in the system, determine the component is available or not.
• Calculate the capacity in that situation.
• Calculate availability with calculated capacity, according to equation 3 (fixed capacity and workload) and add it to availabilitySamples

}

aggregate availabilitySamples

The complexity of the above algorithm is O(M.N), i.e. linear in the number of states. Note that since sampling availability is embarrassingly parallel, you can easily utilize all cores of your machine. To write your own simulator, you can start with this example Go code that simulates the general case of two-server service explained above for S servers.

Conclusion

Availability is very important for service providers. Distributed systems and site reliability engineers must understand the availability of their service to make informed design and operational decisions. In this post, I tried to provide a practical definition for availability and how we can mathematically model and estimate it. I believe having rigorous models is the key to higher hardware efficiency and making insightful decisions.